*Звон школьного колокола перестал быть слышен даже в самых отдаленных уголках замка. Преподаватели, которым не повезло проводить занятия в первый учебный день после каникул, приступили к выполнению своих нелегких обязанностей. Лишь профессор Дэвис продолжала ковыряться в установленном на одной из последних парт механизме, хмуриться и время от времени постукивать по нему волшебной палочкой. Аппарат не хотел работать, Эйн же явно не собиралась отступать. Притихшая аудитория с интересом наблюдала за противостоянием человека, да не простого человека, а целой волшебницы, и машины, да не простой машины, а сделанной магглами*
- Если не будет работать - *обратилась к одному из сидящих за партой чародейка* - Попросите у мисс Блэк - *с этими словами она указала рукоятью палочки на старшекурсницу-гриффиндорку за первой партой*
*Двое учеников: подвижный худощавый равенкловец и его приятель – полноватый медлительный хаффлпаффец, синхронно кивнули*
- Доброе утро, класс - *разобравшись с неисправным механизмом, волшебница быстрым шагом направилась к своему столу* - Надеюсь, каникулы для многих из вас не прошли даром, вы прекрасно отдохнули и сейчас готовы включиться в работу. Материала у нас, как обычно, много, а времени традиционно мало.
*Приблизившись к столу, Эйн обошла его, но садиться не спешила, предпочтя продолжить лекцию стоя*
- В прошлом семестре мы с вами начали изучать нумерологию Древней Греции, но вынуждены были прерваться…
- Потому что изучали маггловские счетные механизмы, которые используются нумерологами - *едва получив разрешение говорить, выпалила одна из третьекурсниц в среднем ряду*
- Именно так, мисс. Кто и как усвоил этот материал, покажет контрольная, которую мы с вам проведем на следующей неделе. Сейчас же вернемся к древнегреческой нумерологии и продолжим изучать различные методики расчета - *переждав тяжкий вздох разочарования, пронесшийся по классу после новости о предстоящей контрольной работе, продолжала Эйн*
- Тот метод, который мы рассмотрим сегодня, широко известен не только волшебникам, но и простецам. Некоторые из них даже активно пользуются им для расчетов. Не будем забывать о том, что раньше волшебники и простецы работали вместе во многих сферах - *повысив голос, продолжала она – несколько слизеринцев начали оживленно перешептываться, явно недовольные тем, что магические знания «эксплуатируются» магглами*
//Это был первый минус на сегодня. И последний для каждого из активистов//- Авторство метода приписывают великому ученому древности, Пифагору, но есть исследователи, которые утверждают обратное – что тот появился гораздо позже и был придуман кем-то из учеников. Быть может, целой группой учеников, которые «привязали» его к громкому имени своего учителя, чтобы окружающие быстрей поверили в нужность и значимость метода. Люди склонны верить авторитетам и прислушиваться к ним.
- Квадрат Пифагора… - *забыв поднять руку, заворожено прошептала девочка лет 12-ти* - Наконец-то…
- Да, сегодня мы говорим о методе, известном под названием «Квадрат Пифагора» - *несдержанность студентки была неприятна волшебнице, но в честь первого учебного дня Эйн решила не наказывать младшекурсницу за нарушение дисциплины* - Личности самого Пифагора на прошлых лекциях внимания уделили достаточно, теперь поговорим о его детище.
- На научную деятельность Пифагора большое влияние оказали труды египетских и вавилонских жрецов-нумерологов. Они первыми задумались о том, как влияют числа на судьбы людей, почему рожденные в один день часто выбирают диаметрально противоположные сферы деятельности. Пифагор развил эту теорию, выяснив, что не только числа, но и буквы имени новорожденного задают, так сказать, тон все его дальнейшей жизни. Он же «гармонизировал» ее, возведя все имеющиеся на тот момент знания в квадрат – почитаемую всеми пифагорейцами фигуру. Символ стабильности и крепкого базиса, без которых любая теория, любой метод будут находиться в шатком и подвешенном положении, что совсем не пойдет им на пользу. Квадрат Пифагора при помощи несложных расчетов давал возможность узнать все необходимое о сильных и слабых сторонах личности, подобрать для нее наиболее оптимальный вид деятельности. Но мы с вами уже говорили о том, что числа не могут указать путь с точностью до малейшего совершенного поступка. Выбор всегда остается за человеком. Если, согласно квадрату, вы наделены прекрасным здоровьем, обладаете достаточной энергией, но так и не стали знаменитым игроком в квиддич, кто в этом виноват: вы сами или «плохой и неправильный» метод?
*Эйн замолчала, давая возможность каждому из студентов ответить на этот вопрос хотя бы самому себе*
- Метод - *первым нарушим тишину хмурый слизеринец крепкого телосложения – прирожденный загонщик* - Чего пообещал, а теперь вот?..
- Вы так думаете, мистер Спаркс? Вы действительно так думаете? - *не дождавшись ответа от студента, переспросила профессор* - Значит, метод должен был помочь Вам оторваться от дивана в общей гостиной, он же должен был вывести вас за ручку из подземелий и заставить хоть раз за все семь лет принять участие в отборе, а после помогать брать мячи без всяких тренировок и усилий с Вашей стороны? В таком случае, это и вправду очень нехороший метод! Тем же, кто не считает его таким уж страшным, могу сказать, что выглядит готовый к анализу квадрат вот так.
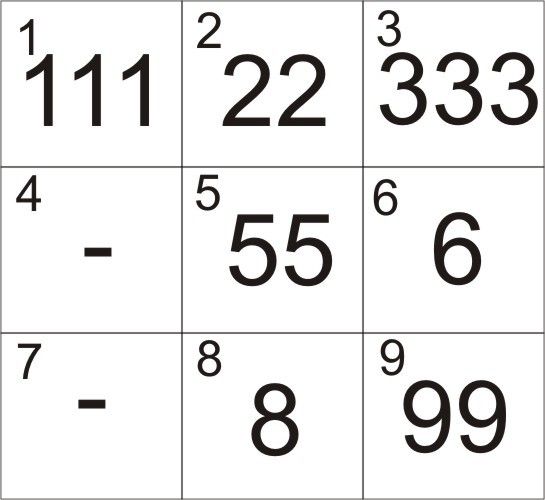
*Девушка указала на доску, расчерченную аккуратными линиями, с заполненными знакомым почерком ячейками. Ни одной буквы на этот раз не было – только арабские цифры*
- Чтобы получить вот такой результат, нужно совсем немного «поколдовать» над собственной датой рождения. А именно сложить или перемножить все числа в ней: день, месяц и год. В более поздних версиях квадрата используются не только даты, но и имена, а их анализ позволяет определить в том числе и уровень владения той или иной стихией, построить графики зависимости жизненных целей от воли, и многое другое. Изучение и анализ квадрата Пифагора давно превратилось в отдельное нумерологическое направление. Поэтому нет ничего удивительного в том, что заложенные ученым азы со временем дополнялись и расширялись. И все же знакомство с методом мы начнем с классического квадрата. Дату возьмем не случайную – год и месяц рождения не менее знаменитой в магическом мире Бриджит Венлок.
*В ящике стола волшебница без труда отыскала нужное - новенькую блестящую карточку от шоколадной лягушки. Так уж сложилось исторически - в качестве учебных пособий преподаватели Хогвартса чаще всего использовали именно коллекционные карточки из любимого лакомства волшебников всех возрастных категорий. Правда, эта карточка не была получена из съеденной Эйн лягушки, а появилась после обмена с одним из коллег чародейки. Что вовсе не мешало ей быть ценной, нужной и завлекательно блестящей. Увеличив предмет и прикрепив его магией к доске, волшебница продолжила*
– Допустим, что нам известны не только месяц и год, но и точный день ее рождения – 11 мая 1202 года.
Метод 1. Общие сведения
1. Складываем все числа дня, месяца и года рождения:
1+1+0+5+1+2+0+2=12
2. Складываем числа полученного результата:
1+2=3
3. Первое рабочее число – 12.
4. Второе рабочее число – 3.
5. Умножаем первую цифру даты рождения на два, даже если человек рожден до 10 числа любого месяца.
1*2=2
6. Вычитаем полученное произведение из первого рабочего числа.
12-2=10
7. Третье рабочее число - 10.
8. Складываем числа полученного результата (третьего рабочего числа) как в пункте 2.
1+0=1
9. Четвертое рабочее число - 1.
10. Записываем числа в два ряда: в первом должна остаться только дата рождения, во втором – четыре рабочих числа.
1 1 0 5 1 2 0 2
1 2 3 1 0 1
11. Теперь в каждую ячейку квадрата записываем только одинаковые цифры из обоих рядов: в первую – единицы, во вторую – двойки. Должно получиться почти так же, как на доске.
Метод 2. Постановка жизненных задач
1. Умножаем число и месяц рождения на год.
1105*1202=1328210
2. Рабочее число – 1328210.
3. В каждую ячейку квадрата записываем только одинаковые цифры из рабочего числа: в первую – единицы, вот вторую – двойки. Все как в первом методе.
Метод 3. Полные сведения
1. Складываем все числа дня, месяца и года рождения:
1+1+0+5+1+2+0+2=12
2. Складываем числа полученного результата:
1+2=3
3. Первое рабочее число – 12.
4. Второе рабочее число – 3.
5. Умножаем первую цифру даты рождения на два, даже если человек рожден до 10 числа любого месяца.
1*2=2
6. Вычитаем полученное произведение из первого рабочего числа.
12-2=10
7. Третье рабочее число - 10.
8. Складываем числа полученного результата (третьего рабочего числа) как в пункте 2.
1+0=1
9. Четвертое рабочее число - 1.
10. Складываем первое и третье рабочие числа.
12+10=22
11. Пятое рабочее число - 22.
12. Складываем второе и четвертое рабочие числа.
3+1=4
13. Шестое рабочее число - 4.
14. Записываем числа в два ряда: в первом должна остаться только дата рождения, во втором – шесть рабочих чисел.
1 1 0 5 1 2 0 2
1 2 3 1 0 1 2 2 4
15. Теперь в каждую ячейку квадрата записываем только одинаковые цифры из обоих рядов: в первую – единицы, вот вторую – двойки, как и в первых двух случаях.
*Записав все необходимое на доске, волшебница стряхнула с рук белую меловую пыль и, решив, что в ногах правды нет, все-таки заняла место за столом*
- В зависимости от того, что именно вы хотите знать о человеке, вам может понадобиться только один метод, но могут пригодиться и все три. Если вам нужно составить представление о человеке лишь в общих чертах, хватит и первого метода. Если важно понять, в какой деятельность способности и таланты человека проявятся лучше всего, чем ему стоит заниматься, лучше всего выбрать второй. И если нужно полное «досье», тогда и только тогда используется третий. Введение двух дополнительных рабочих чисел дает новую информацию для анализа, но делает ее менее точной из-за такого распыления. Ошибиться даже в простых расчетах легко, а при использовании этих методов нужна особая точность: от количества цифр в той или иной ячейке зависит то, насколько сильно те или иные качества развиты у человека. Поэтому считать сегодня будем не вручную, а с помощью вот этих арифмометров - *аккуратно разгладив образовавшиеся на мантии складки, девушка не спеша указала на стоящий на ее столе аппарат*
*Точно такие же были на партах у студентов – по одному на стол, с таким же она возилась и в самом начале занятия*
- Справиться с ними будет проще, чем с арифмометром Лейбница. И носить «Курту» легче. Нужно лишь вспомнить, как она работает.
Сложение
1. Очищаем счётчик результатов (при помощи рычага с кольцом в верхней части арифмометра).
2. Переводим его в крайнее левое положение (так, чтобы он сделал полный оборот и вернулся в исходное положение).
3. Вводим число A (опускаем нужные вертикальные рычаги вниз, ориентируясь по нанесенному в нижней части арифмометра циферблату разрядов. Например, опуская рычаг над цифрой, можно получить от 1 до 9. Те же действия над цифрой 2 дадут результат от 10 до 90. И так далее).
4. Производим сложение (вращаем рычаг с рукояткой).
5. Аналогично вводим число В.
6. Повторяем сложение.
7. Ищем результат в счётчике результатов (находится в верхней части арифмометра, рядом с рычагами, окрашен черным).
Вычитание
1. Очищаем счётчик результатов (при помощи рычага с кольцом в верхней части арифмометра).
2. Переводим его в крайнее левое положение (так, чтобы он сделал полный оборот и вернулся в исходное положение).
3. Вводим число A (опускаем нужные вертикальные рычаги вниз, ориентируясь по нанесенному в нижней части арифмометра циферблату разрядов).
4. Производим сложение (вращаем рычаг с рукояткой).
5. Аналогично вводим число В.
6. Переводим арифмометр в режим "вычитание" (аккуратно приподнимаем рычаг c рукояткой).
7. Производим вычитание (вращаем рычаг с рукояткой)
8. Ищем результат в счётчике результатов (находится в верхней части арифмометра, рядом с рычагами, окрашен черным).
Умножение
1. Очищаем счётчик результатов (при помощи рычага с кольцом в верхней части арифмометра).
2. Переводим его в крайнее левое положение (так, чтобы он сделал полный оборот и вернулся в исходное положение).
3. Вводим множимое (лучше выбрать то, у которого максимальная сумма цифр; используем нужные вертикальные рычаги, ориентируясь по нанесенному в нижней части арифмометра циферблату).
4. Производим сложение несколько раз, пока крайнее значение крайнего правого разряда счётчика оборотов (находится в верхней части арифмометра, рядом с рычагами, окрашен серым) не станет равным крайней правой цифре множителя.
5. Поворачиваем верхнюю часть арифмометра на один разряд вправо.
6. Повторяем пункты 3-4 для второй, третьей и всех остальных цифр множителя до тех пор, пока весь он не окажется в счётчике оборотов (находится в верхней части арифмометра, рядом с рычагами, окрашен серым).
7. Ищем результат в счётчике результатов (находится в верхней части арифмометра, рядом с рычагами, окрашен черным).
- Деление, извлечение корня – все это доступно арифмометру, но рассматривать все его функции мы сегодня не будем – времени до конца урока осталось совсем мало. А вам еще нужно успеть обсчитать свои даты рождения всеми тремя методами, и записать результаты в бланки, которые вы видите на своих столах. Их анализом займемся на следующем занятии. Я советую не терять времени и приступать к работе прямо сейчас. Никому ведь не хочется задерживаться на перемене в первый же учебный день?
*Усердный скрип перьев о пергаменты и тихое пощелкивание рычагов арифмометров послужило ответом чародейке. Похоже, желания уделить любимой Нумерологии лишних 5 минут свободного времени не возникло даже у фанатов учебного процесса. Уже к началу перемены в классе не осталось ни одного ученика. А на рабочем столе мисс Дэвис – ни одного свитка со свежим домашним заданием*
Задания
- Коротко ответьте на следующие вопросы своими словами:
- Почему до сих пор не утихают споры по поводу авторства квадрата Пифагора?
- Что можно узнать при помощи квадрата Пифагора?
- Почему нельзя рассчитать классический квадрат Пифагора, зная лишь имя и фамилию человека?
- Сколько ячеек в квадрате?
- Сколько всего рабочих чисел в первом методе рассчета? Сколько во втором и третьем? - На лекции профессор поспорила со студентом о том, кто же больше виноват в неудачах: сам человек или квадрат, посуливший ему всевозможные блага. А как вы думаете, кто виноват или что виновато в ваших неудачах и нереализованных возможностях? Подумайте и порассуждайте.
- (Эта лекция только для 1, 2, 3, 4, 5, 6, 7 курсов)
Дополнительные задания
- Доклад «Квадрат и его предки». Расскажите о древних египетских и вавилонских методиках расчета, легших в основу квадрата Пифагора. (1000 символов)
- Ролевой отыгрыш «Забыть
Герострата Пифагора!». После занятий вы случайно сталкиваетесь в библиотеке с Томми Спарксом – тем самым студентом-слизеринцем с лекции, несостоявшейся звездой квиддича. Он настроен очень серьезно и собирает свою собственную студенческую организацию «ОКО» - Общество КвадратоОбиженных. По мнению самого Спаркса, квадрат Пифагора не просто вреден, но и крайне опасен, так как дает волшебникам ложное чувство уверенности в собственных силах и фальшивые надежды. Маг собирается уничтожить любое упоминание квадрата, предать забвению любое учение о нем, и планирует начать с мисс Дэвис, которая должна прекратить рассказывать студентам о квадрате Пифагора. Вам предложено войти в состав группы, которая должна «поговорить» с ней по душам. Чем же закончился этот странный «разговор», я хочу узнать из ваших работ.
- Задание на фантазию. На лекции профессор рассказывала о трех способах расчета при помощи квадрата Пифагора. Придумайте еще 3 метода, но таких, чтобы в них обязательно использовались число, месяц и год рождения. Копирование методов из лекции баллов не принесет.
- Сочинение «Труд, который облагораживает». Всем известно, что профессор Дэвис – большая поклонница устного счета. Даже самые сложные расчеты она обычно призывает делать в уме, в крайнем случае на бумаге, но никак не с помощью счетных механизмов. И вдруг… Довольно простой квадрат Пифагора профессор призывает обсчитывать при помощи арифмометра. Как вы думаете, к чему такие «сложности» в простых расчетах? И действительно ли все дело только в точности результатов и желании избежать ошибок, или есть другие причины? Почему вы так думаете?
- (Эта лекция только для 1, 2, 3, 4, 5, 6, 7 курсов)