*Если бы кому-нибудь пришло в голову снимать магический и фантастический фильм «Машина времени в ванне старост», лучшими декорациями для него послужил бы сегодняшний кабинет Нумерологии. Каждый дюйм ровной поверхности был занят той или иной вычислительной машиной. Для нынешнего занятия мисс Дэвис удалось раздобыть не только школьные арифмометры с яркими инвентарными номерами на деревянных боковинках, но и многие другие счетные механизмы*
- В прошлый раз мы с вами изучили древнейшие счетные механизмы разных народов - *по звону колокола начала лекцию преподаватель*
- Ничего себе древнейшие! Соробаном же до сих пор пользуются - *тихо возмутилась старшекурсница-гриффиндорка, сидящая за второй партой крайнего левого ряда*
*Ее соседка – студентка того же факультета, согласно закивала*
- Рада, что Вы внимательно слушали и усвоили материал прошлой лекции, мисс - *громче шептуний отметила Эйн* - Но мне почему-то кажется, что кое-что важное Вы все же упустили.
- Э… Нужно было поднять руку? – *заливаясь румянцем в цвет герба на мантии, уточнила чародейка*
- Именно, мисс - *подтвердила ее догадку профессор* - Так вот, на сегодняшнем занятии мы с вами изучим более новые и совершенные счетные механизмы, многие из которых используются нумерологами и по сей день - *с этими словами девушка обвела взглядом кабинет, ненадолго задержав его на одном особенно массивном аппарате*
-
1623 год подарил всему миру замечательнейшее изобретение
немецкого математика, астронома и востоковеда Вильгельма Шиккарда – «Считающие часы». Это устройство стало первым в истории механическим калькулятором. То есть, устройством для выполнения арифметических и логических операций над числами и алгебраическими формулами - *поспешила объяснить недоумевающим чистокровным волшебникам значение слова «калькулятор» Эйн* - Само слово произошло от греческого термина «calculus», что переводится как «счет», «исчисление». Тогда как «calculator» – это «счетчик».
- Профессор - *вытягивая руку вверх так, что даже кончики пальцев задрожали, заерзал на своем месте пухлый светловолосый хаффлпаффец*
- Но ведь часы не считают, они просто показывают время - *получив разрешение говорить, выпалил он*
- И так, и не так, мистер Хорнер - *внимательно выслушав вопрос паренька, ответила мисс Дэвис* - Стрелки часов действительно помогают нам узнать точное время. Но посмотрите внимательно: минутная стрелка не сдвинется с места, пока секундная не «отсчитает» ровно 60 секунд. Часовая стрелка – пока минутная не «отсчитает» ровно 60 минут. Но «Считающими часами» механизм был назван не за это. В нем активно использовались шестеренки и звездчатые детали, по своему устройству аппарат был очень похож на обычный часовой ангренаж. Таким образом, можем говорить о том, что «Считающие часы» Шиккарда работали на зубчатой передаче. Механизм мог производить над числами основные арифметические действия: сложение, вычитание, умножение и деление. Притом только сложение и вычитание – автоматически. Среди нумерологов Европы изобретение Вильгельма Шиккарда не нашло особого распространения, но зато им с большим удовольствием пользовался друг ученого – знаменитый астроном Иоганн Кеплер. О нем вам должны были рассказывать или еще расскажут на уроках Астрономии, мы же с вами просто посмотрим, как выглядели эти самые старинные «Часы».
*Пройдя в самый конец класса, волшебница остановилась у свободной парты. Ее поверхность занимал небольшой аппарат в деревянном корпусе, но с круглыми бронзовыми ручками. Выдвижные «язычки» по обоим бокам механизма были пронумерованы от 2 до 9*
- А вот упрощенный чертеж устройства, выполненный самим ученым. Мюнхенские маги из «Немецкого музея достижений естественных наук и техники» любезно согласились одолжить его для сегодняшнего занятия. Можете подойти и посмотреть, но только аккуратно - *предупредила чародейка*
//Эти немецкие маги еще педантичнее Дейнза//- Естественно, «Считающие часы» были первой, но далеко не последней попыткой и магов, и магглов облегчить расчеты - *после того, как изучившие чертеж студенты вновь заняли свои места, продолжила лекцию профессор*
-
В 1642 знаменитый механик, математик, физик, литератор и философ Блез Паскаль начал создание своей собственной
суммирующей машины, позже названной в честь него
«Паскалиной». На тот момент ему было 19 лет. Мсье Паскаль был блестящим теоретиком и выдающимся практиком во всем, что не касалось магических наук. Рожденный в семье простецов, он так и не смог овладеть практическими навыками колдовства – даже самое безобидное заклинание в его исполнении вызывало совершенно непредсказуемые последствия. Так, в замке академии магии Шармбатон до сих пор сохранилась башня, называемая студентами «башней Блеза» - она дважды разрушалась едва ли не до самого основания при простых попытках Паскаля применить заклинание Люмос. И оба раза ее отстраивали заново. В теории юному чародею не было равных: любые сочинения, контрольные и тесты он сдавал лучше всех студентов своего курса, но когда дело доходило до практики… - *девушка многозначительно замолчала, давая живому воображению слушателей возможность дорисовать жуткие картины последствий колдовства молодого Паскаля* - Будучи от природы человеком умным, волшебник здраво рассудил, что при таком уровне владения палочкой в волшебном мире ему делать нечего. Сдав выпускные экзамены в Шармбатоне с небывалыми для школы результатами: высшими баллами за теоретическую часть и низшими – за практическую, он вернулся в привычный с детства мир магглов. Многие ученые до сих пор спорят о том, как мог такой гениальный в теории магии человек, оказаться настолько плохим практиком. Некоторые из них считают, что на самом деле Блез Паскаль обладал исключительным по своей силе магическим даром, который просто не сумел до конца подчинить себе.
//А иные полагают, что всему виной маггловская кровь//*Мысленно добавила Эйн, однако озвучивать не стала – теория была довольно популярна, но лишь в определенных узких кругах чистокровных нумерологов*
- Как бы там ни было, отсутствие волшебной палочки не помешало Блезу создать свою знаменитую «Паскалину». В ней, как и в «Считающих часах», использовалась зубчатая передача: небольшой корпус машины был под завязку заполнен валами и шестеренками. Посмотрите на верхнюю панель.
*С этими словами волшебница подошла к одному из подоконников, место которого сегодня досталось странного вида металлической коробке с колесиками*
- При помощи этих наборных колес и водились числа. Их всего девять, каждое из них соответствует одному разряду: единицами, десяткам, сотням, тысячам и так далее. На каждом колесе вы можете видеть деления от 0 до 9. Таким образом, для ввода числа достаточно было выбрать разрядность колеса и прокрутить его до нужного деления. Однако при полной прокрутке колеса получившийся «избыток» переносился на соседнее, сдвигая его на одно деление. В первой версии «Паскалины» было всего 5 колес: единицы, десятки, сотни, тысячи, десятки тысяч. Но позже Блез добавил колес, получив сначала 6, а затем и 8 наборных элементов. Это позволило его «Паскалине» работать с очень большими по тому времени числами – вплоть до 9 999 999. Наборные колеса вращались только в одном направлении, поэтому работать с отрицательными числами «Паскалина» не могла. А вот в этих металлических окошках выводился ответ - *профессор указала на прорези прямо над наборными колесами*

- Только сложение, скукотища - *с самым кислым видом резюмировал темноволосый слизеринец, вяло поднимая руку сразу же вслед за комментарием*
- А кто Вам сказал, что суммирующая машина могла выполнять только сложение? - *глядя на ученика в упор, поинтересовалась мисс Дэвис*
- Ну так суммирующая же - *вновь откликнулся неугомонный ученик*
*С его логикой было трудно спорить, и все же чародейка возразила:*
- Да, Паскаль выбрал не самое удачное название для своего детища. Возможно, потому что сложение у его машины получалось лучше всего, однако она также могла вычитать и умножать числа. Правда, эти действия сопровождались не самой удобной процедурой набора. Так, для вычитания использовалось так называемое «дополнение до девятки», а промежуточные результаты вычислений отображались вот в этом дополнительном окошке. А для умножения – очень громоздкая процедура повторных сложений. Был и ряд других трудностей – использование десятичной системы счисления в «Паскалине» делало ее практически непригодной для действующей в то время маггловской денежной системы Франции. На родине Паскаля были в ходу ливры, су и денье. В каждом ливре было 20 су, в каждом су – 12 денье.
- На наши галеоны, сикли и кнаты похоже - *пискнул кто-то из младшекурсников среднего ряда*
- Да, определенное сходство есть - *признала девушка* - Но о том, почему наша денежная система так похожа на старинные денежные системы магглов, вам лучше расскажет моя коллега – мисс Винтерхелл. Пока же вернемся к нашим «Паскалинам». Не связанные денежными отношениям магглов нумерологии, благосклонно приняли изобретение Паскаля. Из созданных им 50 экземпляров, 10 выкупили именно они. Кроме того, отец мага, работавший сборщиком налогов, по достоинству оценил изобретение сына, ведь именно его трудная и утомительная счетная работа вдохновила юного Блеза на создание «Паскалины». А заложенный в конструкцию машины принцип связанных колес, не только стал революционным для своего времени, но и долгие годы использовался создателями других счетных механизмов.
*Дождавшись, пока все желающие пощупают и изучат «Паскалину» со всех сторон, Эйн продолжила лекцию*
- Новым словом в истории вычислительной техники стало появление
в 1673 году арифмометра, разработанного знаменитым
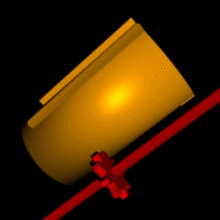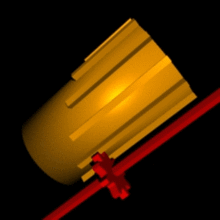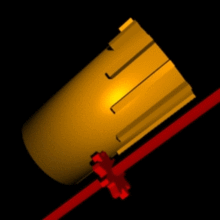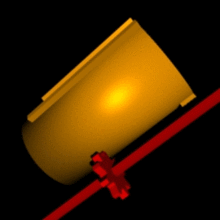
немецким математиком, физиком, философом, историком и изобретателем Готфридом Вильгельмом Лейбницем. К этому его подтолкнуло знакомство с голландским физиком, математиком, изобретателем и астрономом Христианом Гюйгенсом ван Зёйлихемом. «Это недостойно таких замечательных людей, подобно рабам, терять время на вычислительную работу, которую можно было бы доверить кому угодно при использовании машины», - отметил он, наблюдая за тем, сколько различных вычислений приходится выполнять астроному при наблюдении за ночным небом. Арифмометр Лейбница, как и «Считающие часы» Шиккарда, мог складывать, вычитать, перемножать и делить числа, используя для этого десятичную систему счисления. Притом для сложения чисел использовалась система связанных колес, впервые реализованная в «Паскалине». В первую версию арифмометра Лейбница были добавлены специальные движущая часть и рукоятка (модель оказалась малоразрядной и непригодной для практического применения). Подобная конструкция позволила ускорить автоматическое многократное сложение чисел при их умножении. Позже она была заменена на изобретенный ученым привод – шагающий цилиндр или же «колесо Лейбница».
*Легким взмахом палочки профессор отправила на доску крупную колдографию*
- Этот привод использовался во многих счетных машинах ни много ни мало 300 лет, вплоть до 1970 года. Что же из себя представлял этот цилиндр?
*На этот раз взмах палочки отправил на доску обычный неподвижный плакат*
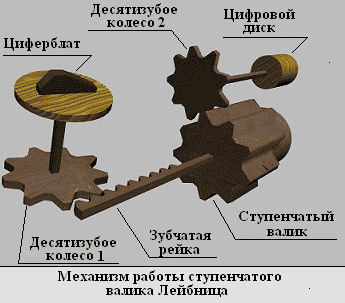
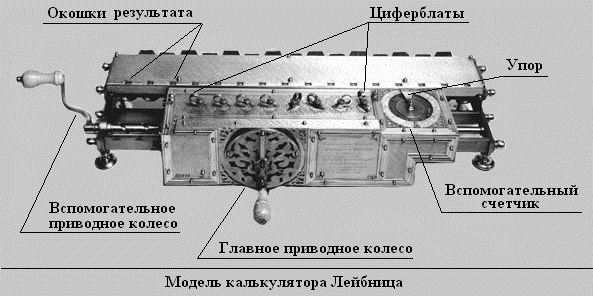
- Посмотрите: на его боковой поверхности, параллельно образующей, располагаются зубья различной длины. К нему крепится другая деталь – зубчатая рейка. Рейка сцепляется с третьей деталью – десятизубым колесом №1. Колесо связано с циферблатом, на поверхность которого нанесены цифры от 0 до 10. Поворачивая циферблат, мы тем самым задаем соответствующий разряд множимого. Например, мы хотим умножить число 27. Второй разряд множимого в этом случае равен 7. Тогда десятизубое колесо № 1, сцепленное с зубчатой рейкой, так переместит цилиндр, что при повороте на 360 градусов он войдет в зацепление с десятизубым колесом № 2 только семью наиболее длинными ребрами. Следовательно, десятизубое колесо №2 повернется на семь частей полного оборота, на столько же повернется и связанный с ним цифровой диск, который отображает результирующее значение выполненной операции. При следующем обороте цилиндра на цифровой диск снова перенесется семерка. В том случае, если цифровой диск совершал полный оборот, результат переполнения переносился на следующий разряд. Поворот цилиндров осуществлялся при помощи ручки главного приводного колеса. Такой подход существенно облегчил процесс машинного умножения: отныне не требовалось вводить множимое много раз – можно было ввести один, и повернуть ручку главного приводного колеса ровно столько раз, на сколько необходимо произвести умножение. Для уменьшения времени на умножение больших чисел, Лейбниц разработал систему сдвига множимого - отдельного умножения на единицы, десятки, сотни и так далее. Для этого пришлось разделить устройство на две части: подвижную и неподвижную. Неподвижную часть заняли цилиндры устройства ввода множимого и основной счетчик. Подвижную - установочная часть устройства ввода множимого, главное приводное колесо и вспомогательный счетчик. Вспомогательное приводное колесо использовалось для восьмиразрядных и более множителей. Трехчастный вспомогательный счетчик существенно облегчал не только умножение, но и деление. На его внешней неподвижной части нанесены цифры от 0 до 9для отсчета количества сложений множимого при произведении операции умножения. Между цифрами 0 и 9 находится специальный упор, предназначенный для остановки вращения вспомогательного счетчика, когда штифт достигнет упора. Подвижная средняя часть вспомогательного счетчика служит для отсчета количества сложений при умножении и вычитаний при делении. На ней имеется десять отверстий напротив цифр внешней и внутренней частей счетчика, в которые и вставляется штифт для ограничения вращения счетчика. Неподвижная внутренняя часть предназначена для отчета количества вычитаний при выполнении операции деления. На ней так же, как и на внешней части, нанесены цифры от 0 до 9, но в обратном порядке. При полном повороте главного приводного колеса средняя часть вспомогательного счетчика поворачивается на одно деление. Если предварительно вставить штифт, например, в отверстие напротив цифры 6 внешней части вспомогательного счетчика, то после шести оборотов главного приводного колеса этот штифт наткнется на неподвижный упор и остановит вращение главного приводного колеса. Можете подойти и осмотреть арифмометр Лейбница – это точная копия, два оставшихся оригинала достать очень сложно - *показывая красивый блестящий прибор с множеством ручек, установленный на профессорском столе, предложила чародейка*

- Принцип расчета при помощи арифмометра Лейбница мы рассмотрим в конце урока, пока же поговорим о том, чем же дальше радовала нумерологов научная мысль магов и магглов. После изобретения Лейбницем своего арифмометра, многие ученые занимались лишь его усовершенствованием. Так появились 16-разрядная машина Вагнера и Левина, арифмометры Тоблера и Буркхардта (1710 год), усовершенствованные версии Кнутцена и Мюллера и многие другие.
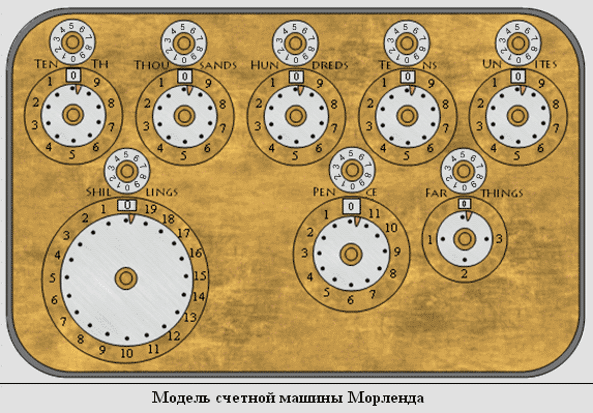
В 1674 году увидела свет
счетная машина Морленда, которая, в отличие от своих предшественников, не смогла предложит ничего принципиально нового ни в методике расчета, ни в конструктивном плане.
В 1709 –
арифмометр де Полени. Его автор –
итальянский физик, математик и астроном Джованни де Полени, сумел изготовить механизм практически целиком и полностью из дерева, к тому же использовать в нем целых два новшества: зубчатое колесо с изменяемым количеством зубьев и внешний источник энергии для полноценной работы механизма (падающий груз). Принцип колес с изменяемым количеством зубьев позже был использован знаменитым механиком и автором одного из арифмометров Вильгодтом Теофильдом Однером. Шестиразрядный арифмометр де Полени не нашел широкого практического применения у магглов именно из-за своих ограниченных возможностей по диапазону вводимых чисел – всего до 199 999, однако среди нумерологов эта модель пользовалась очень большой популярностью. Многие мои коллеги до сих пор производят расчеты именно с его помощью. Кому интересно – может подойти поближе - *указала волшебница на второй занятый непонятной конструкцией подоконник*
В 1820 году был выпущен
первый серийный механический калькулятор Карла Ксавье Томаса из Кольмара. Себестоимость производства арифмометров к тому времени значительно упала, что позволило сделать их более доступными для широкого круга пользователей.
- В то время как самому Лейбницу производство его арифмометра обошлось в 24 000 таллеров (зарплата одного маггловского министра той поры составляла порядка 1000-2000 таллеров).
С 1900 годов XX века начинается самый настоящий арифмометро-бум. Эти счетные механизмы выпускаются любых форм и размеров: настольные, наколенные, напольные и даже карманные (
«Curta» 1948 года выпуска, разработка
австрийского инженера Курта Херцштарка).
*Девушка указала на неприметный черный приборчик, буквально теряющийся на фоне массивного механизма Лейбница*
- Эта портативная модель широко используется многими нумерологами и в наши дни. Арифмометры выпускались на колесе Однера и валике Лейбница, могли быть автоматическими и неавтоматическими. И даже записывающими результат на бумажной ленте – арифмографами. Так сказать, на любой вкус. Каждый нумеролог мог подобрать себе помощника как по цене, так и по набору необходимых для работы функций. С 1900 года все арифометры умели выполнять 4 базовые операции: сложение, вычитание, умножение и деление. Отличие заключалось лишь в быстродействии, диапазоне доступных для набора чисел и уровне автоматизации. Автоматические арифмометры многие действия могли выполнять самостоятельно, но стоили примерно в 2 раза дороже неавтоматических. Первый полностью автоматический арифмометр был выпущен в 1919 году. Вот он - Mercedes-Euklid VII - *показала нужный аппарат чародейка*

- А вот некоторые образцы арифмометров той поры. На то, чтобы разместить и посмотреть их все, нам бы не хватило кабинета. Закончим все же веком XIX, двумя российскими моделями:

Арифмометр П.Л.Чебышёва

Арифмометр В.Т.Однера
- А вот прямой потомок арифмометра Однера:

Арифмометр «Феликс»

Арифмометр Mercedes Euklid 37MS

Неавтоматический клавишный арифмометр Nisa K2

Арифмометр Facit CA 1-13

Автоматический арифмометр Friden SRW, способный извлекать квадратные корни чисел

Автоматический арифмометр Rheinmetall SAR, гордость Германии - один из лучших арифмометров того времени
*Взглянув на наручные часы, Эйн обнаружила, что времени до звонка как раз хватит для того, чтобы рассмотреть арифмометра Лейбница в действии*
- А теперь самое интересное – немного практики - *негромко хлопая ладонью по столу, чтобы успокоить расшумевшихся у машин и аппаратов ребят, продолжила мисс Дэвис*
- Итак, что же мы делаем, если хотим сложить два числа? А делаем мы вот что:
1. Устанавливаем циферблаты в нужные положения, и таким образом вводим первое слагаемое.*Аккуратно покрутив ручки, девушка без проблем добилась нужного результата*
2. Поворачиваем ручку главного приводного колеса. Да-да, вот эту большую и одинокую на передней панели, один раз по часовой стрелке.*Легко обернув ручку, профессор перешла к выполнению следующего пункта*
3. Вводим второе слагаемое точно так же, как и первое.*На этот раз волшебница действовала чуть быстрей – ребята уже видели процедуру ввода, а лекционное время было ограничено*
4. Еще раз аккуратно крутим ручку приводного колеса и вот – получаем результат в специальном окошке. - Такой простой алгоритм - *закончив демонстрацию, резюмировала чародейка*
- Алго… что? - *послышалось сразу несколько недоуменных шепотков*
- Алгоритм. Такая штука, на которой маггловские компьютеры работают - *с чувством огромного внутреннего превосходства громко, на всю аудиторию, поделился своими познаниями вихрастый первокурсник с синей нашивкой на мантии*
- И не только они, мистер Дэннисон - *поспешила поправить слишком активного студента профессор*
//Сын специалиста в области IT?//-
Алгоритм – это особый набор инструкций, описывающих порядок действий исполнителя для достижения результата за конечное число действий, при любом наборе исходных данных. Любая достаточно подробная инструкция, направленная на достижение какого-либо результата, может быть названа алгоритмом. Рецепты зелий и лимонного безе – это тоже алгоритмы. Ведь что такое рецепт зелья или пирога? Это подробнейшая пошаговая инструкция того, что нужно делать зельевару или повару для того, чтобы получить желаемое – сладость или зелье. Вы сталкиваетесь с алгоритмами на каждом шагу, просто не обращаете на это внимания. План подготовки к экзамену – тоже алгоритм.
//Пяти- и семикурсники наверняка поймут меня//- Некоторые вычисления по дате рождения – алгоритм. Примеров можно привести множество, но самые интересные я надеюсь увидеть в ваших домашних работах. Термин принято связывать с именем
математика из Хорезма Абу Абдуллаха Мухаммеда ибн Муса аль-Хорезми. Алгоритм – аль-Хорезми. При изрядной доле фантазии можно услышать некоторое созвучие.
- Вторым человеком, с именем которого в волшебном мире принято связывать понятие алгоритма, является
Августа Ада Кинг, графиня Лавлейс (урожденная Байрон). Единственная законнорожденная дочь поэта Джорджа Гордона Байрона. Будучи волшебницей, мать девочки долгое время не могла признаться творческому и впечатлительному мужу в том, кто же она на самом деле. Единожды отвергнув предложение руки и сердца, она была уверена в том, что проблем с этим ухажером более не возникнет. Однако Джордж оказался настолько настойчив, что молодые люди вскоре поженились. За увлечение математикой и нумерологией, Байрон даже называл свою молодую супругу «королевой параллелограммов». Но семейная идиллия продлилась недолго – застав однажды свою супругу за колдовством, Джордж потребовал объяснений. Получив их, мужчина не смог принять жену-волшебницу и подал документы на развод. Августу Аду, названную в честь его сестры, он видел лишь один раз в жизни - через месяц после рождения девочки. Униженная и оскорбленная женщина, впала в глубокую депрессию, сопровождающуюся неконтролируемыми магическими выбросами. Родители чародейки приняли решение отправить дочь отдохнуть и подлечиться, взяв все заботы о новорожденной внучке на себя. Отдых и лечение заняли по разным сведениям от 6 до 8 лет. Вернувшаяся обратно в Англию леди Байрон, наотрез отказалась отправлять дочь в Хогвартс, предпочтя нанять ей лучших репетиторов, которых только можно было достать. Унаследовавшая математические способности матери Ада, делала большие успехи в нумерологии. Очень скоро она начала переводить научные труды лучших ученых Европы на родной английский язык, а также составлять алгоритмы для вычислений при помощи счетных машин. Так, например, ею была создана программа для расчета чисел Бернулли на машине Бэббиджа. Несмотря на домашнее образование, волшебница была очень эрудированным человеком, знакомым со многими выдающимися людьми своей эпохи. Магглы ценят графиню Лавлейс как выдающегося математика и первого в истории программиста. Маги – как автора ряда научных трудов по нумерологии. В том числе и трудов, посвященных вычислениям при помощи счетных механизмов. Ее сочинениями в свое время увлекалась знаменитая нумеролог Бриджит Венлок. Младший из сыновей миссис Кинг – Ральф Гордон Кинг, единственным из трех детей унаследовал магический дар матери и бабушки, и основал в Косом переулке фирму «R.G.K Inc». Его компания вот уже много лет занимается изготовлением и продажей счетных механизмов, а также написанием программ под некоторые из них, являясь практически монополистом на рынке подобных товаров и услуг. Сейчас ею заведует прапраправнук сэра Ральфа – Брайан Кристофер Кинг. Быть может, мы как-нибудь посетим его магазин в Магическом Лондоне. Прелюбопытнейшее зрелище… Для истинных ценителей - *снова сверяясь с часами – до звонка оставалась ровно одна минута, закончила Эйн*

- История развития маггловской вычислительной техники на этом не закончилась, но современные электронные приборы в магическом мире не используются, поэтому для волшебников с окончанием эры арифмометров развитие счетных приборов остановилось. Однако следует отметить, что с нумерологическими вычислениями и они прекрасно справляются. А сейчас можете разбирать свитки с новым домашним заданием и уже проверенные работы, и на сегодня быть свободны - *отпустила подуставших студентов чародейка*
Задания
- Ролевой отыгрыш урока (можно целиком, можно только практическую часть) с обязательным использованием арифмометра Лейбница и описанием последовательности действий (как в лекции).
Слизерин – 36+67
Гриффиндор – 47+62
Равенкло – 85+14
Хаффлпафф – 27+54 - (Эта лекция только для 1, 2, 3, 4, 5, 6, 7 курсов)
Дополнительные задания
- Сочинение «Дешево и сердито». Представьте себя молодым нумерологом, который только-только окончил Хогвартс. Работы пока что нет, деньги на исходе, но желание заниматься именно Нумерологией вас не покинуло. И вам для работы необходим счетный механизм. В магазине продавец предлагает на выбор более дешевую ручную модель с ограниченным диапазоном вводимых чисел и полностью автоматизированную, с большим диапазоном, но внушительной ценой. Что вы выберете? Почему? Объясните свой выбор.
- Доклад о любом маггловском техническом средстве, которое может быть использовано в работе нумеролога. Примеры из лекции не брать. (1500 символов)
- Ролевой отыгрыш «Конкурентное преимущество». Вы решили открыть в Британии свой собственный небольшой бизнес по продаже арифмометров. Но вот беда – монополист на рынке, компания «R.G.K Inc», может изрядно помешать вашим планам. Под покровом темноты вы пробираетесь в лавку, чтобы «позаимствовать» кое-какие наработки компании и тем самым обеспечить успех своему предприятию. О том, чем же закончилась эта история, я хочу узнать из ваших работ.
- Задание на фантазию. Выберите любой из предложенных вариантов и напишите подробный алгоритм к нему. Можно оформить в виде РО.
- Я иду в Косую аллею покупать все необходимое к началу учебного года;
- Я планирую ночную вылазку из гостиной, чтобы пойти в Запретный лес/Кухню/Запретную секцию библиотеки/Ванну старост;
- Я планирую свой бюджет в 2 галеона на ближайший поход в Хогсмид, чтобы посетить «Три метлы», «Сладкое королевство» и «Зонко».
Примечание: Если во втором варианте задания вы собираетесь посетить за ночь сразу несколько мест, это не может не повлиять на ваш алгоритм.
- (Эта лекция только для 1, 2, 3, 4, 5, 6, 7 курсов)