*Учеников в классе нумерологии заметно поубавилось, но опоздавших в этот раз не было. К началу урока все желающие уже были на месте. Занятая проверкой домашних работ профессор, казалось, вовсе не обращала внимания на студентов. Но стоило школьному колоколу напомнить о начале занятий, как девушка отложила в сторону последний пергамент и поднялась из-за стола*
- Рада снова видеть большинство из вас. А тому, что сегодня никто не опоздал, рада вдвойне. В прошлый раз мы с вами начали осваивать очень важный материал, но не успели. Поэтому сегодня нам предстоит как следует потрудиться, чтобы наверстать упущенное.
*Очередным взмахом палочки волшебница поместила на столы студентов письменные принадлежности и приготовилась рассказывать дальше, но…*
- Мистер Бэйтс, Вы хотите что-то спросить? - *обратилась она к рослому слизеринцу, поднявшему руку вверх*
- Мисс Дэвис, а когда можно будет узнать оценки за домашнее задание?
- В конце урока я верну вам ваши свитки, и каждый сможет увидеть собственные баллы. Они достаточно высоки, многие из вас постарались и ответственно подошли к выполнению домашнего задания. Надеюсь, так будет всегда, а не только в первый раз. Я ответила на Ваш вопрос, мистер Бейтс? Если да, предлагаю вернуться к нашей нумерологии. У нас действительно очень много работы.
*Отточенным движением палочки, вытащив из кипы плакатов нужный, Эйн прикрепила его к доске*
| | 1 (для записи единиц первых шести десятков) |
| | 3 (пример записи числа 1-го десятка) |
| | 10 (для записи первых шести десятков) |
| | 20 (пример записи числа 2-го десятка) |
| | 32 (пример записи числа 4-го десятка) |
| | 59 (пример записи числа 6-го десятка) |
| | 60 (для записи чисел седьмого, восьмого, девятого десятков и сотен) |
| | 302 (пример записи сотен) |
| | 0 (для записи отсутствующего разряда) |
| | 3600 (для записи тысяч) |
| | 7203 (пример записи тысяч) |
| | 180 (при отсутствии низшего разряда) |
- Разобраться в этой системе счисления будет непросто. Громоздкая шестидесятеричная система счисления Древнего Вавилона сложна и неудобна в использовании. Но все же очень важна для понимания некоторых аспектов нумерологии, потому что этой науке вавилоняне уделяли большое внимание. Многие открытия были сделаны именно ими. Примерно 40 веков назад в Вавилоне появилась уникальная позиционная нумерация. При такой нумерации одна и та же цифра может обозначать разные числа. Ее значение будет зависеть от занимаемого положения. То есть, цифра, стоящая в начале записи, может обозначать, например, 100, а стоящая в конце – 10. Та нумерация, которой мы с вами пользуемся изо дня в день, тоже позиционная. Позиционная система счисления характеризуется целым числом b>1, называемым основанием системы счисления. Однако у нас основанием служит число 10 (b=10, десятеричная система счисления), а у вавилонян его роль выполняло число 60 (b=60, шестидесятеричная система счисления). Числа меньше 60 и больше 60 в вавилонской нумерации изображались по-разному. Так, единицы чисел до 60 изображались вот так:

. А десятки так:
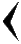
. Такая форма цифр называется клинописью и связана с тем, что жители Вавилона вели свои записи треугольными палочками на глиняных табличках. Все знаки при необходимости повторялись нужное число раз. Так, для того, чтобы записать число 3, нужно было три раза изобразить цифру

.
Обратите внимание на запись числа 59: десятки – слева, единицы – справа. Все как в современной нумерации. Впрочем, запись чисел больше 60 тоже мало чем отличается от нашей. Цифры «разбиваются» по разрядам, разряды отделяются друг от друга небольшими пробелами. От разряда к разряду значение клинышка возрастает, но не в 10 раз, как привыкли мы, а в 60. Потому что древние вавилоняне, как вы, надеюсь, запомнили, пользовались именно шестидесятиричной системой. Рассмотрим число 302.
*Нижняя часть доски еще не была занята многочисленными плакатами и именно на ней профессор принялась записывать пример*
- Сотни записаны слева, как и положено (60+60+60+60+60=60*5=300), десятки – справа (1+1=1*2=2). Между ними есть небольшой зазор, чтобы не запутаться. Интереснее дело обстоит в том случае, если какой-либо из разрядов пропущен. Тогда использовали вот такой знак:
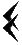
. Он должен был играть роль нуля. Вот пример такой записи – число 7203:
- Тысячи, как положено, находятся слева, сотни отсутствуют, их заменяет тот самый знак ((60+60)*60=2*60*60=7200), а единицы занимают в записи числа крайнее правое положение (1+1+1=1*3=3). Существенный недостаток вавилонской нумерации заключался в том, что низший разряд, как правило, не записывался. Так, например, число 180 (60+60+60=3*60=180) писали просто:
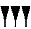
- При этом обозначать такая запись могла все что угодно – от 3 и 180 до 10800 (3*60*60=10800). Понять, какое же именно число имел в виду автор записи, можно было только по смыслу текста. Доподлинно известно, что изначально жители Вавилона пользовались десятеричной системой счисления (об этом свидетельствует форма записи чисел до 60 – они записываются по принципу чисел в десятеричной системе). Как, когда именно и почему вавилоняне перешли на шестидесятеричную систему, неизвестно. Десятки исследователей пытались разгадать эту загадку, строились многочисленные гипотезы, однако ни одна из них так и не была подтверждена. Шестидесятеричная запись целых чисел не нашла широкого применения – она была распространена лишь в пределах Ассиро-Вавилонского царства. Но шестидесятеричные дроби активно использовались учеными Средней Азии, Ближнего Востока, Западной Европы и Северной Африки. Широкое распространение эти дроби получили в астрономии. Они были популярны вплоть до появления десятичных дробей, и лишь в XVII веке начали постепенно сдавать свои позиции. Но даже в наши дни следы шестидесятеричной вавилонской системы отыскать не так уж трудно: наш час состоит из 60 минут, а минута – из 60 секунд.
*Задумавшись о чем-то, девушка не сразу продолжила рассказ*
- Так. Теперь давайте обратимся к системам счисления народов Южной Америки.
*Сменив один плакат на другой, профессор вновь взялась за пояснение*
| | 1 |
| | 2 |
| | 3 |
| | 4 |
| | 5 |
| | 6 |
| | 7 |
| | 8 |
| | 9 |
| | 10 |
| | 11 |
| | 12 |
| | 13 |
| | 15 |
| | 19 |
| | 20 |
- Сразу хочу сказать: эта нумерация уникальна. Если народы Старого Света так или иначе заимствовали системы счисления и нумерации друг у друга, то майя и ацтеки придумывали свои собственные практически с нуля. Пятеричная система счисления позже была заменена двадцатеричной, и нумерация было спешно «переделана» под нее. В основу двадцатеричной системы легло количество пальцев рук и ног. Кроме ацтеков и майя, этой системой пользовались кельты, населявшие Западную Европу со II тысячелетия до нашей эры. Ее отголоски можно увидеть и в наши дни. Так, например, они хорошо видны в денежной системе магглов. В одном франке (денежной единице Франции до 1999 года) ровно 20 су. А числительное восемьдесят звучит как quatre-vingts, то есть «четырежды двадцать». Однако вернемся к нумерации майя. Именно ее вы сейчас видите на доске. Записывались числа в столбик. Начиналась запись со знака

, затем следовал знак

, а уже после него

. От большего к меньшему. Из чего мы можем сделать вывод о том, что в отличие от позиционной вавилонской системы, эта система счисления аддитивна. Примеры записи чисел нумерацией майя вы можете видеть ниже.
*Малознакомые южноамериканские цифры в исполнении волшебницы, вновь оккупировали свободную часть доски*



(5) +

(5) +

(5) +

(1) = 16.



(20) +

(1) +

(1) +

(1) = 23.
- Следующая система, которую мы с вами должны рассмотреть, одна из старейших в мире.
*Очередной плакат отправился на доску, заняв центральное место*

- Понять, какому народу принадлежит данная нумерация, не так уж сложно. Она появилась около 4000 лет назад в Китае. Несмотря на то, что эта нумерация такая древняя, она намного опередила собственное время. Китайскую нумерацию заслуженно называют самой прогрессивной нумерацией Древнего мира. В ее основе лежат принципы, используемые в современных системах счисления. Китайские иероглифы препятствовали появлению аддитивной системы, поэтому древним ученым мужам пришлось хорошенько подумать, как выйти из столь незавидного положения. Результатом их размышлений и стало появление мультипликативной системы счисления. Мультипликативной называется такая система счисления, в которой значение каждой цифры зависит от ее положения в записи числа, и для его прочтения требуется использовать не сложение, а умножение. Цифры в китайской нумерации записывались от большего в к меньшему, однако говорить о том, что такая система аддитивна, уже не приходится. Если какой-либо разряд не был указан, его просто пропускали и писали следующий, но это было не совсем удобно. Именно поэтому во времена династии Мин (1368-1644 годы) для пустующих разрядов был введен специальный знак – небольшой кружок вроде всем знакомого нуля. Для того чтобы не перепутать разряды, использовали особые служебные иероглифы: они ставились после основного иероглифа-цифры и указывали его значение в конкретном разряде. Сравните:
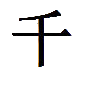
(1000) и
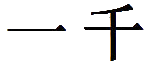
(1000). В каждом случае это число записывается по-разному, но каждая запись имеет право на существование. Пример записи чисел китайской нумерацией на доске.
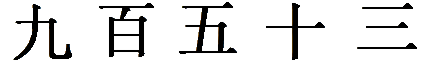
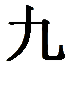
(9) *

(100) +
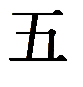
(5) *
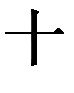
(10) +
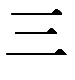
(3) = 953.
- Не думаю, что стоит грузить вас произношением всех этих страшных иероглифов - *усмехнулась девушка* - поэтому предлагаю перейти к рассмотрению не менее интересной нумерации.
| | 1 |
| | 5 |
| | 10 |
| | 30 |
| | 100 |
| | 1000 |
| | 10 000 |
| | 100 000 |
| | 1 000 000 |
| | 10 000 000 |
- Эта нумерация появилась в Древнем Египте около 5000 лет назад. Египетскую нумерацию называют древнейшей из всех известных человеку. Обозначения в ней довольно просты: числа от 1 до 10 изображаются вертикальными черточками.
//Да уж, не слишком оригинально//- Притом те из них, для написания которых требуется несколько таких вот палочек, записываются в два ряда. Палочек в каждом из них должно быть либо поровну, либо больше в нижнем ряду. Числа от 10 до 100 изображаются подковообразной дугой. Ученые всего мира до сих пор спорят, что же это на самом деле: человеческая пятка или же символическое изображение пут, которыми древние египтяне связывали скот. Сколько десятков нужно было изобразить, столько «подковок» и записывали. Например, число 90 изображали в виде 9 подковок. Для числа 100 был создан специальный знак – веревка. Такой мерной веревкой древние египтяне измеряли земельные участки после того, как воды Нила возвращались в прежнее русло. Число 1000 тоже удостоилось персонального знака – это цветущий лотос. Почему именно это число удостоилось чести изображаться при помощи священного символа египтян, я надеюсь узнать из ваших домашних работ. Число 10 000 слишком велико для того, чтобы относиться к нему легкомысленно. Об этом напоминает и поднятый вверх указательный палец, изображающий это число. Головастик, изображающий число 100 000, символизирует несметное количество этих земноводных на берегах Нила. Если бы вы случайно увидели в собственном сейфе Гринготтса целую гору золотых галлеонов, то, наверное, очень бы удивились этому. Примерно так рассуждали и египтяне, изображающие человека с воздетыми к небу руками в качестве цифры 1 000 000. 10 000 000 – наибольшее (на тот момент) число, которое египтяне изображали в виде восходящего солнца, посвятив его тем самым богу Ра.
- Древние египетские иероглифы записывались слева направо, от большего к меньшему. Если какой-то разряд отсутствовал, его просто пропускали и писали дальше. Запрещалось использование девяти одинаковых иероглифов в записи одного числа. Пример записи чисел египетской иероглифической нумерацией:
*В этот раз девушка записывала числа гораздо дольше*
- Естественно, такая нумерация была не слишком удобна в использовании. Поэтому спустя тысячу лет египтянами была разработана иератическая нумерация. Эти упрощенные иероглифы были более удобны в использовании и не требовали большого количества времени для записи. В 650 году до нашей эры иератическую нумерацию вытеснила еще более совершенная демотическая.
*Звон школьного колокола подвел итог нынешней лекции. Мисс Дэвис выглядела уставшей, но очень довольной*
//Основные нумерации и системы счисления мы изучили, а с остальными чуть позже познакомимся//- Не забудьте записать домашнее задание и забрать свитки с предыдущим. Порадуйте наконец-то собственное любопытство.
Задания
- Один из студентов на лекции поддался лени и не стал подробно записывать выдаваемую мисс Дэвис информацию. А теперь и сам запутался в собственных записях. Как вы думаете, о каких нумерациях здесь идет речь? Аргументируйте.
- Всего 3 значка
- Кругляшки, палки, точки
- Иероглифы какие-то
- Самые древние веселые картинки - В аддитивной системе счисления обычно действует правило «не больше энного количества цифр в одной записи». Как вы думаете, есть ли аналогичные ограничения в мультипликативных системах счисления? Почему вы так считаете?
- (Эта лекция только для 1, 2, 3, 4, 5, 6, 7 курсов)
Дополнительные задания
- Ролевой отыгрыш «Культурный обмен». Вы – жрец из племени майя, встретили в родных джунглях странного оборванца. Он что-то лопочет на непонятном вам языке, тычет в свои лохмотья и о чем-то просит. Похоже, плав.средство бедолаги потерпело крушение, его выбросило на берег. В поисках разумных живых существ он добрел сюда. Несмотря на то, что незнакомец не говорит на вашем языке, он считает так же, как и вы – при помощи двадцатеричной системы счисления. Постарайтесь узнать о пришельце как можно больше до того, как его принесут в жертву.
- Сочинение. Следы вавилонской системы счисления легко отыскать в современном летоисчислении, следы нумерации майя – в действовавшей до недавнего времени денежной системе, китайской мультипликативной – в современном алфавите. И только следы египетской остались лишь на стенах пирамид да в папирусных свитках. Как вы думаете, почему же ей не нашлось места в современном мире? Порассуждайте.
- Доклад «Особенности алфавита». Расскажите о том, какие именно языковые особенности помешали созданию китайской аддитивной системы счисления. (1500 символов)
- Задание на фантазию. Вы – вождь маленького, но очень гордого племени со своими традициями, культурой и даже нумерацией. Ваши земли вот-вот завоюют орды чужеземцев, в которых народ просто «растворится». Придумайте способ сохранить свою культуру и нумерацию. Задание можно оформить в виде ролевого отыгрыша.
- (Эта лекция только для 1, 2, 3, 4, 5, 6, 7 курсов)













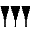
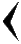
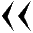
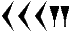
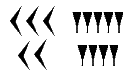

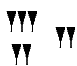
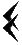

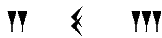
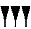
 . А десятки так:
. А десятки так: 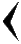 . Такая форма цифр называется клинописью и связана с тем, что жители Вавилона вели свои записи треугольными палочками на глиняных табличках. Все знаки при необходимости повторялись нужное число раз. Так, для того, чтобы записать число 3, нужно было три раза изобразить цифру
. Такая форма цифр называется клинописью и связана с тем, что жители Вавилона вели свои записи треугольными палочками на глиняных табличках. Все знаки при необходимости повторялись нужное число раз. Так, для того, чтобы записать число 3, нужно было три раза изобразить цифру  .
.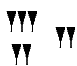
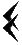 . Он должен был играть роль нуля. Вот пример такой записи – число 7203:
. Он должен был играть роль нуля. Вот пример такой записи – число 7203: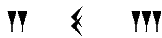
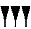
















 , затем следовал знак
, затем следовал знак  , а уже после него
, а уже после него  . От большего к меньшему. Из чего мы можем сделать вывод о том, что в отличие от позиционной вавилонской системы, эта система счисления аддитивна. Примеры записи чисел нумерацией майя вы можете видеть ниже.
. От большего к меньшему. Из чего мы можем сделать вывод о том, что в отличие от позиционной вавилонской системы, эта система счисления аддитивна. Примеры записи чисел нумерацией майя вы можете видеть ниже.



 (20) +
(20) +  (20) +
(20) +  (5) +
(5) +  (5) +
(5) +  (5) +
(5) +  (1) +
(1) +  (1) +
(1) +  (1) +
(1) +  (1) = 59.
(1) = 59.

 (5) +
(5) +  (5) +
(5) +  (5) +
(5) +  (1) = 16.
(1) = 16.

 (20) +
(20) +  (1) +
(1) +  (1) +
(1) +  (1) = 23.
(1) = 23.
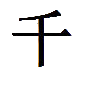 (1000) и
(1000) и 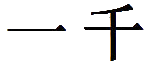 (1000). В каждом случае это число записывается по-разному, но каждая запись имеет право на существование. Пример записи чисел китайской нумерацией на доске.
(1000). В каждом случае это число записывается по-разному, но каждая запись имеет право на существование. Пример записи чисел китайской нумерацией на доске.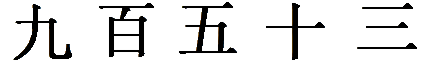
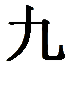 (9) *
(9) *  (100) +
(100) + 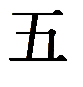 (5) *
(5) * 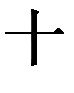 (10) +
(10) + 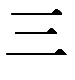 (3) = 953.
(3) = 953.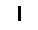
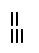






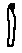

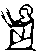
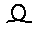



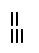
 (100) +
(100) +  (10) +
(10) +  (10) +
(10) + 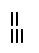 (5) = 125.
(5) = 125.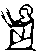
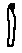
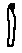





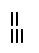
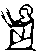 (1 000 000) +
(1 000 000) + 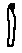 (10 000) +
(10 000) + 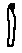 (10 000) +
(10 000) +  (1000) +
(1000) +  (1000) +
(1000) +  (1000) +
(1000) +  (10) +
(10) +  (10) +
(10) + 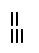 (5) = 1 023 025
(5) = 1 023 025












